Suppose you need to simulate an effect that happens \(p = 1/four\) of the time, and all you have is a fair coin. Well, that'due south easy enough. Flip the coin twice. Report success if you lot become 2 heads, and written report failure otherwise.

Suppose \(p = ane/iii\) instead. That may not be a power of two, only there is still a simple solution. Flip the fair coin twice. Written report success on HH, report failure on HT or Thursday, and try again on TT. Each iteration takes \(2\) coin flips, and there is a \(iii/4\) probability of halting, giving \(8/iii\) expected coin flips.

Now, suppose you need to simulate \(p = 1/10^{100}\). Well, aught is peculiarly wrong with the current scheme. We need \(\lceil\log_2(x^{100})\rceil = 333\) coin flips to go enough outcomes. And then, label \(1\) case every bit success, \(ten^{100} - 1\) as failure, and the rest as retries. For analyzing runtime, these numbers are starting to get messy, but we can at least ballpark the expected number of flips. The probability of halting is \(> 1/2\), since past structure \(2^{332} < x^{100} < two^{333}\), pregnant the number of retry cases is less than half of all cases. Thus, the expected number of flips is at most \(666\). Yes, that is…

(•_•) ( •_•)>⌐■-■ (⌐■_■)

a devilish upper leap, but things could be worse.

(I'one thousand not sorry.)

Simply, what if you need to simulate \(p = 1 / 10^{10^{100}}\)? Or simulate \(p = i/\pi\)? In the first case, the number of flips needed is enormous. In the second, the scheme fails completely - there is no way to simulate irrational probabilities.

Like shooting fish in a barrel Optimizations

We'll get back to the irrational example later.

Recall how nosotros faux \(p=1/4\). The scheme reports success but on HH. So, if the first flip lands tails, we tin can halt immediately, since whatever way the second money lands, we volition report failure anyways. The revised algorithm is

  • Flip a money. If tails, written report failure.
  • Flip a coin. Report success on heads and failure on tails.

This gives \(3/2\) expected flips instead of \(2\) flips.

As another example, consider \(p = one/v\). Starting time, plan to flip 3 coins. Divide the 8 outcomes into one success example, 4 failure cases, and 3 retry cases. These can exist distributed every bit

  • accept: HHH
  • failing: THH, THT, TTH, TTT
  • retry: HHT, HTH, HTT

If the first coin is T, we can cease immediately. If the beginning two coins are HT, nosotros can retry immediately. The only case left is HH, for which we need to run into the third flip before deciding what to do.

(Some of you may be getting flashbacks to prefix-complimentary codes. If yous haven't seen those, don't worry, they won't testify up in this post.)

With clever rearrangement, we can bundle outcomes of a given type under as few unique prefixes as possible. This gives some improvement for rational \(p\), merely withal does non let u.s.a. simulate irrational \(p\). For this, we need to switch to a new framework.

A New Prototype

I did non come up with this method - I discovered it from hither. I wish I had come with it, for reasons that will go articulate.

Allow \(p = 0.b_1b_2b_3b_4b_5\ldots\) be the binary expansion of \(p\). Proceed as follows.

  • Flip a coin until it lands on heads.
  • Let \(n\) exist the number of coins flipped. Report success if \(b_n = 1\) and report failure otherwise

The probability the process stops after \(n\) flips is \(1/two^northward\), so the probability of success is

\[P[success] = \sum_{northward: b_n = 1}^\infty \frac{1}{ii^n} = p\]

Regardless of \(p\), it takes \(2\) expected flips for the coin to land heads. Thus, whatever biased coin can be fake in \(two\) expected flips. This beats out the other scheme, works for all \(p\) instead of but rational \(p\), and all-time of all yous can compute bits \(b_i\) lazily, making this implementable in real life and not but in theory.

Slick, correct? This idea may accept been obvious to you, but information technology certainly wasn't to me. After thinking nearly the problem more, I somewhen recreated a potential concatenation of reasoning to reach the same result.

$.25 and Pieces

(Starting now, I will use \(1\) interchangeably with heads and \(0\) interchangeably with tails.)

Consider the following algorithm.

  • Construct a real number in \([0,1]\) by flipping an space number of coins, generating a random number \(0.b_1b_2b_3\ldots\), where \(b_i\) is the outcome of coin flip \(i\). Allow this number be \(x\).
  • Study success if \(x \le p\) and failure otherwise.

This algorithm is correct every bit long equally the decimals generated follow a uniform distribution over \([0, 1]\). I won't testify this, but for an appeal to intuition: any 2 bit strings of length \(k\) are generated with the same probability \(1/ii^k\), and the numbers these stand for are evenly distributed over the interval \([0, 1]\). As \(k \to\infty\) this approaches a uniform distribution.

Bold this all sounds reasonable, the algorithm works! But, there is the small problem of flipping \(\infty\)-ly many coins. However, similarly to the \(p = 1/iv\) example, nosotros can stop coin flipping as soon every bit as it is guaranteed the number will fall in or out of \([0, p]\).

When does this occur? For now, limit to the instance where \(p\) has an infinite binary expansion. For the sake of an example, suppose \(p = 0.1010101\ldots\). In that location are 2 cases for the first flip.

  1. The coin lands \(1\). Starting from \(0.ane\), it is possible to fall inside or outside \([0,p]\), depending on how the next flips go. The algorithm must continue.

  2. The coin lands \(0\). Starting from \(0.0\), information technology is impossible to fall outside \([0,p]\). Even if every coin lands \(ane\), \(0.0111\ldots_2 = 0.1_2 < p\). (This is why \(p\) having an space binary expansion is important - it ensures at that place will be another \(one\) down the line.) The algorithm can halt and report success.

So, the algorithm halts unless the coin flip matches the \(1\) in \(p\)'southward expansion. If information technology does not match, it succeeds. Consider what happens next. Starting from \(0.1\), in that location are 2 cases.

  1. Side by side coin lands \(1\). Since \(0.11 > p\), we can immediately report failure.
  2. Next coin lands \(0\). Similarly to before, the number may or may non end in \([0,p]\), so the algorithm must continue.

So, the algorithm halts unless the coin flip matches the \(0\) in \(p\)'s expansion. If information technology does not match, it fails. This gives the post-obit algorithm.

  • Flip a money until the \(due north\)th coin fails to match \(b_n\)
  • Report success if \(b_n = one\) and failure otherwise.

Note this is substantially the same algorithm every bit mentioned above! The only difference is the catastrophe condition. Instead of halting on heads, the algorithm halts if the random bit does not match the "true" chip. Both happen \(1/2\) the time, so the two algorithms are equivalent.

(If you wish, you can extend this reasoning to \(p\) with finite binary expansions. Just make the expansion infinite by expanding the trailing \(ane\) into \(0.1_2 = 0.0111\ldots_2\).)

Hither's a sample run of the algorithm told in pictures. The greenish region represents the possible values of \(ten\) every bit bits are generated. Initially, any \(ten\) is possible.

0 to 1

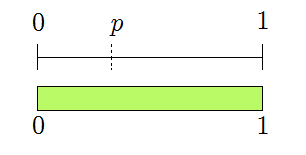
The first generated bit is \(0\), reducing the valid region to

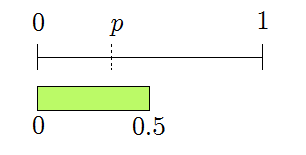
0 to 0.5

This still overlaps \([0,p]\), so continue. The 2nd bit is \(1\), giving

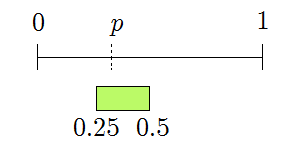
0.25 to 0.5

This nonetheless overlaps, so keep. The tertiary scrap is \(1\), giving

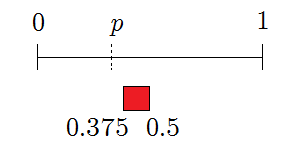
0.375 to 0.5

The feasible region for \(10\) no longer intersects \([0,p]\), so the algorithm reports failure.

CS-minded people may see similarities to binary search. Each flake chooses which half of the viable region nosotros motility to, and the halving continues until the feasible region is a subset of \([0,p]\) or disjoint from \([0,p]\).

Proving Optimality

This scheme is very, very efficient. Simply, is it the all-time we can do? Is there an algorithm that does meliorate than \(2\) expected flips for general \(p\)?

It turns out that no, \(2\) expected flips is optimal. More surprisingly, the proof is not too bad.

For a given \(p\), whatever algorithm tin be represented past a computation tree. That tree encodes whether the algorithm succeeds, fails, or continues, based on the adjacent scrap and all previously generated $.25.

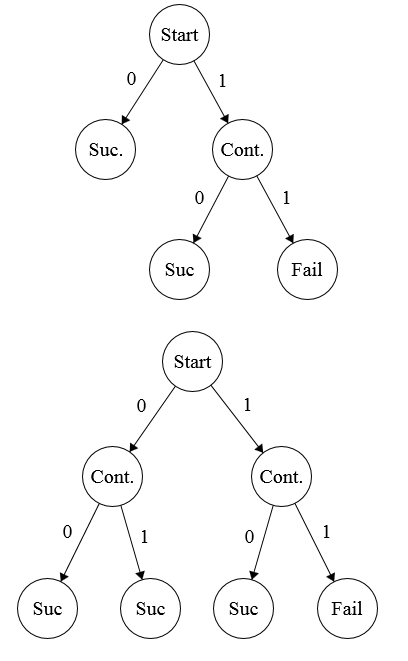
Computation trees

Two sample computation trees for \(p = iii/four\).

With the convention that the root is level \(0\), children of the root are level \(i\), and then on, allow the weight of a node be \(1/ii^{\text{level}}\). Equivalently, the weight is the probability the algorithm reaches that node.

For a given algorithm and \(p\), the expected number of flips is the expected number of edges traversed in the algorithm'due south computation tree. On a given run, the number of edges traversed is the number of vertices visited, ignoring the root. By linearity of expectation,

\[Due east[flips] = \sum_{5 \in T, five \neq root} \text{weight}(v)\]

To be correct, an algorithm must end at a success node with probability \(p\). Thus, the sum of weights for success nodes must be \(p\). For \(p\) with infinitely long binary expansions, we must have an infinitely deep computation tree. If the tree had finite depth \(d\), whatsoever leafage node weight would exist a multiple of \(ii^{-d}\), and the sum of success node weights would accept at most \(d\) decimal places.

Thus, the computation tree must exist infinitely deep. To be infinitely deep, every level of the tree (except the root) must take at least 2 nodes. Thus, a lower jump on the expected number of flips is

\[E[flips] \ge \sum_{k=i}^\infty 2 \cdot \frac{one}{ii^k} = two\]

and as nosotros take shown earlier, this lower bound is achievable. \(\blacksquare\)

(For \(p\) with finite binary expansions, you can do meliorate than \(2\) expected flips. Proving the optimal spring for that is left every bit an exercise.)

In Conclusion…

Every coin in your wallet is now an arbitrarily biased fleck generating machine that runs at proven-optimal efficiency. If you run into a bridge troll who demands you simulate several flips of a money that lands heads \(1/\pi\) of the time, you lot'll exist ready. If you lot don't, at least you know i more interesting thing.